How does Frobenius and spectral norm grow?
Interested in behavior of following random quantities with $B$ Gaussian samples stacked as rows of $X$:
- Frobenius norm: $\|XX^T\|_F$
- Spectral norm: $\|XX^T\|$
- Spectral norm ratio $\alpha_\text{max}$: $\frac{2B}{\|XX^T\|}$
- Frobenius norm ratio $\alpha_\text{opt}$: $\frac{B \|X\|_F^2}{\|XX^T\|_F^2}$
Last two quantities correspond to 2 different methods of setting per-batch step size for noiseless overparameterized least squares SGD (see details) and in simulations on Gaussian data are potentially perfectly predicted by 2 formulas involving effective ranks of generating distribution. code
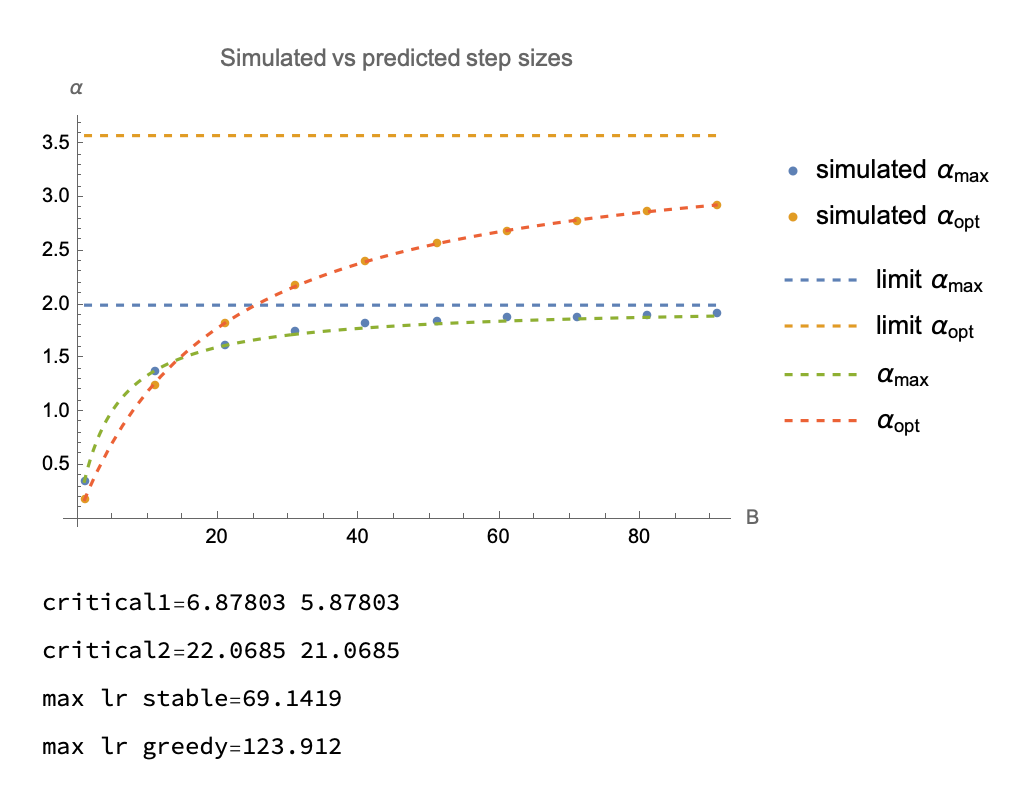
Formulas involve "effective ranks" r and R of generating distribution.
$$\begin{align}\label{ranks}r=&\frac{\text{Tr}\Sigma}{\|\Sigma\|}\\R=&\frac{(\text{Tr}\Sigma)^2}{\text{Tr}\Sigma^2}\end{align}$$These $r$ and $R$ match Definition 3 from Srebro's "Uniform Convergence" paper. (r also in occurs in many places, in Belkin's paper page 34, Nick Harvey notes, Tropp has a whole Chapter on it, Chapter 7 in survey)
In particular, the following relation seems to hold for $\alpha_\text{max}$
$$ \begin{align} \frac{B}{\alpha_B^\text{max}}&=\frac{1}{\alpha_1^\text{max}}+\frac{B-1}{\alpha_\infty^\text{max}}\\ \alpha_\infty^\text{max}&=\frac{2r}{E[\|x\|^2]}\\ \alpha_1^\text{max}&=\frac{2}{E[\|x\|^2]}\\ \end{align} $$The following relation seems to holds for $\alpha_\text{opt}$
$$ \begin{align} \frac{B}{\alpha_B^\text{opt}}=&\frac{1}{\alpha_1^\text{opt}}+\frac{B-1}{\alpha_\infty^\text{opt}}\\ \alpha_1^\text{opt}&=\frac{1}{E[\|x\|^2]}\\ \alpha_\infty^\text{opt}&=\frac{R}{E[\|x\|^2]}\\ \end{align} $$