Why condition number doesn't matter
Take classical problem in 2D, the Rosenbrock function. This problem is ill-conditioned, and you have a high probability of landing in a narrow valley, which makes your gradient descent perform poorly.
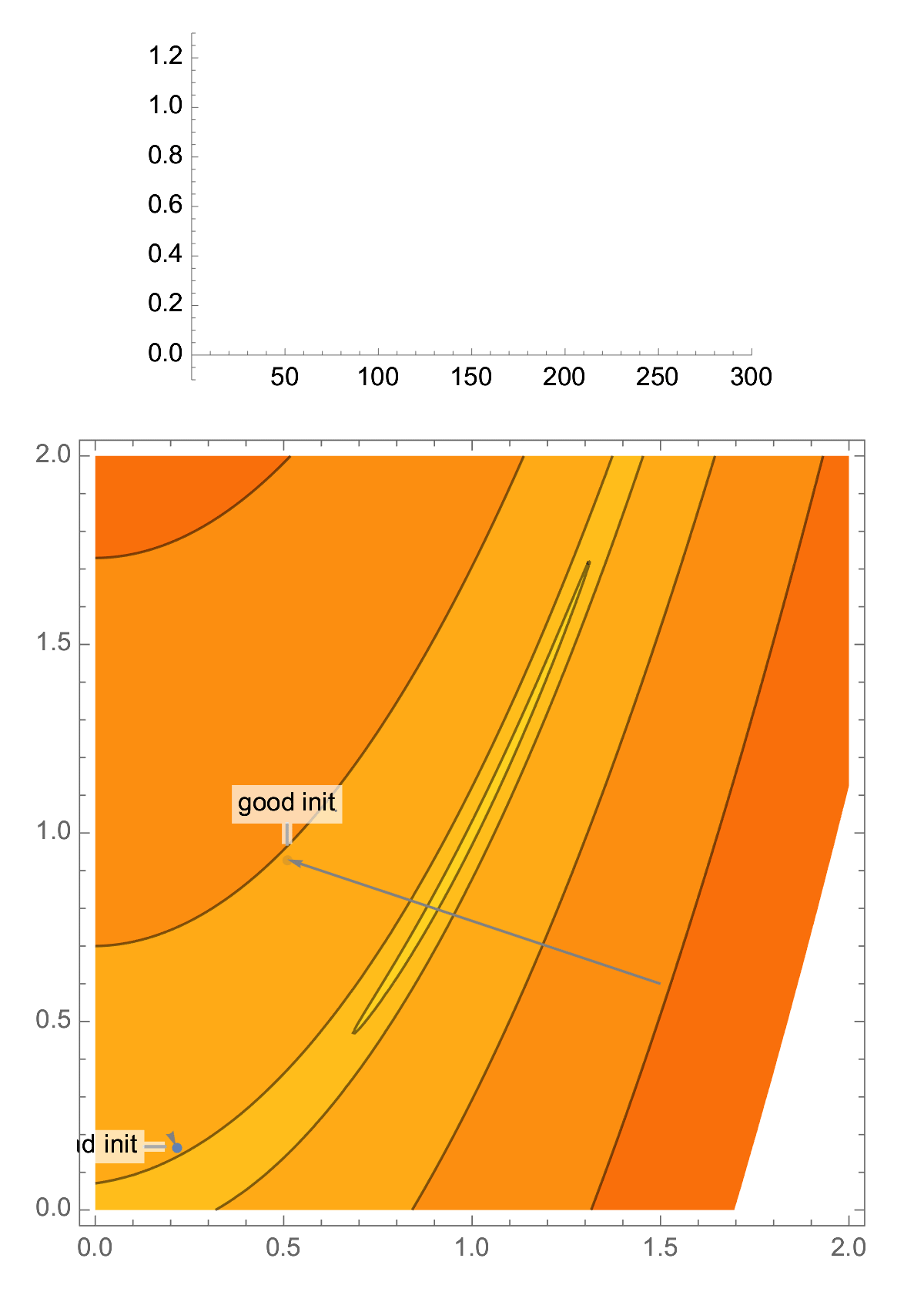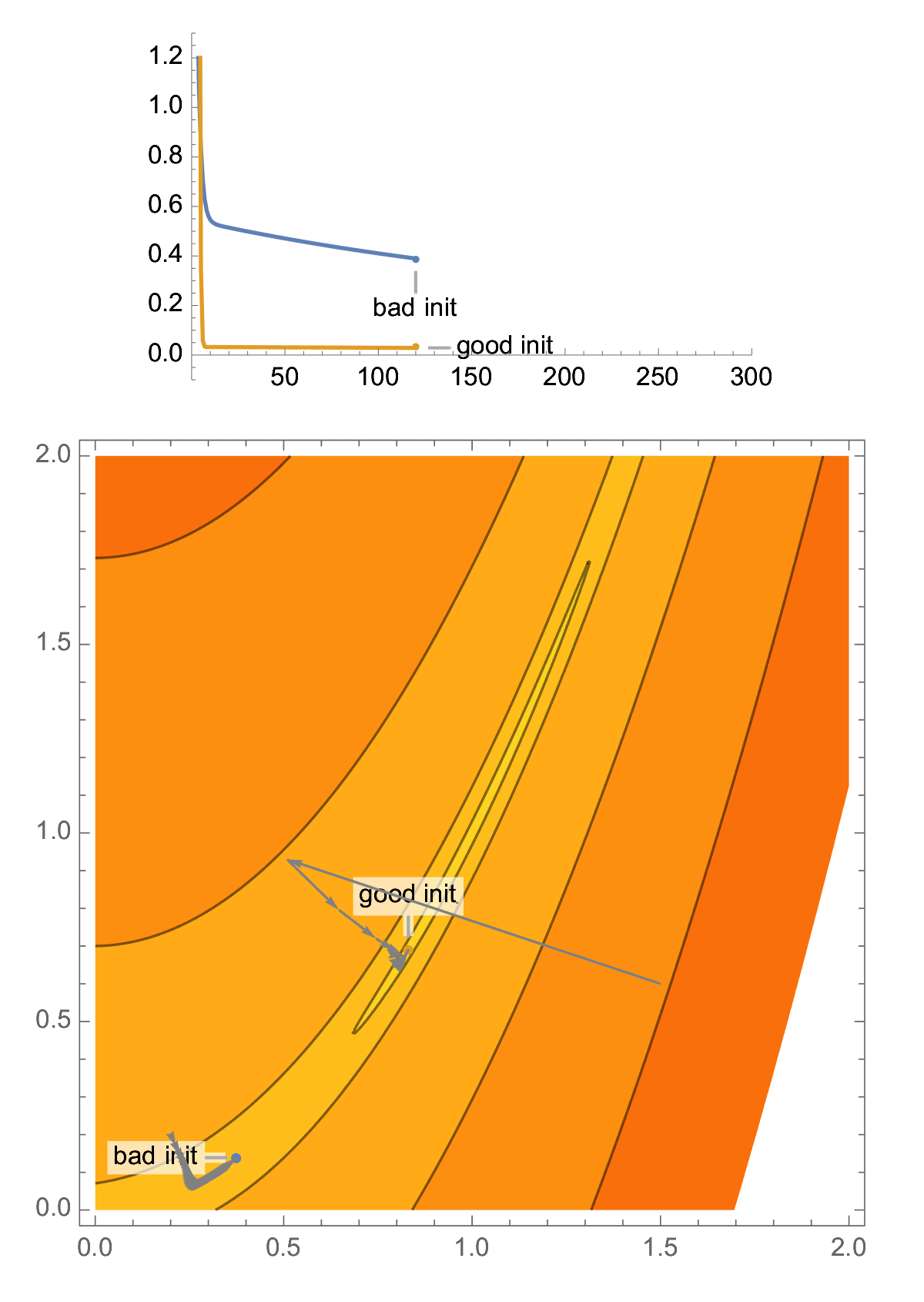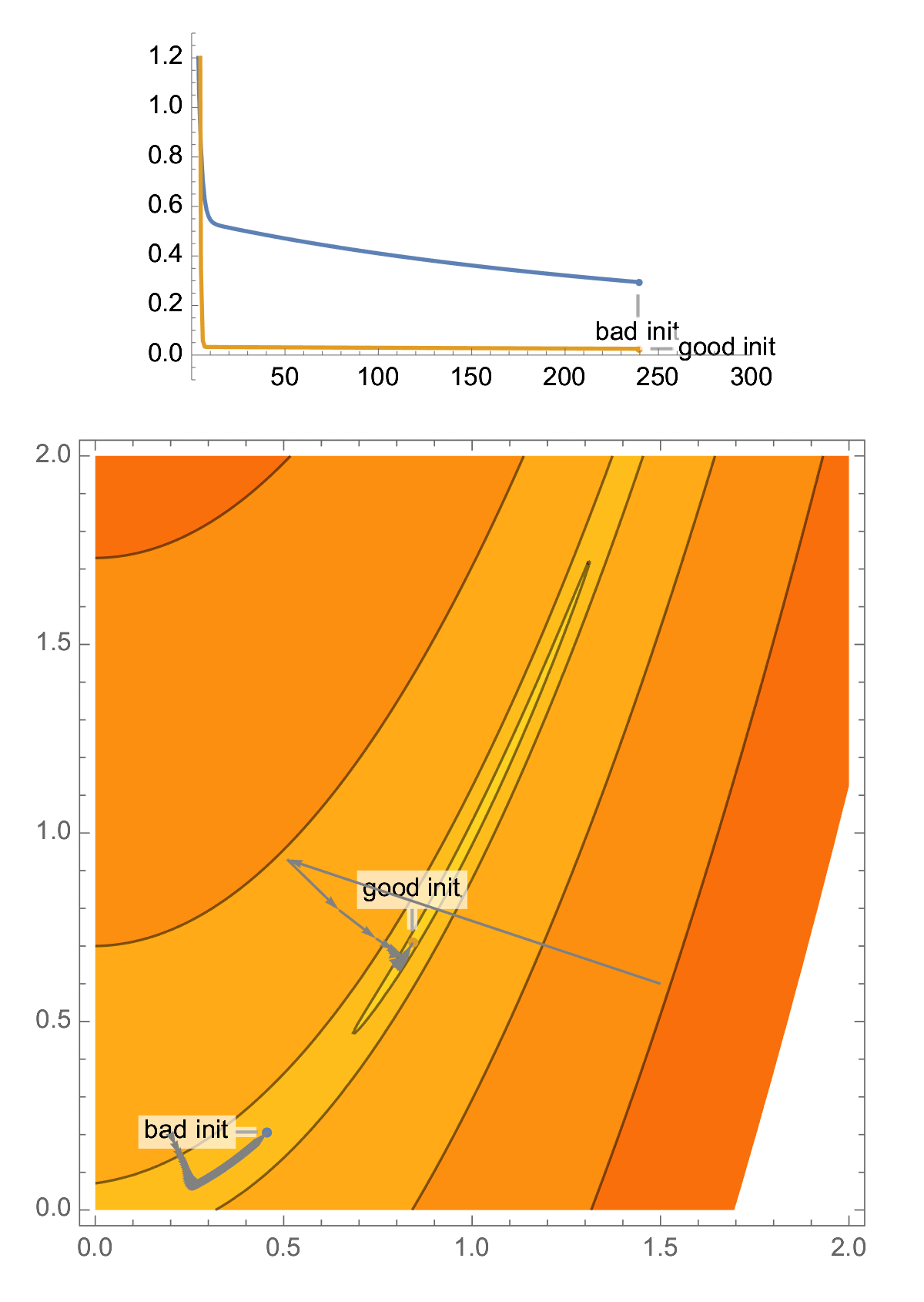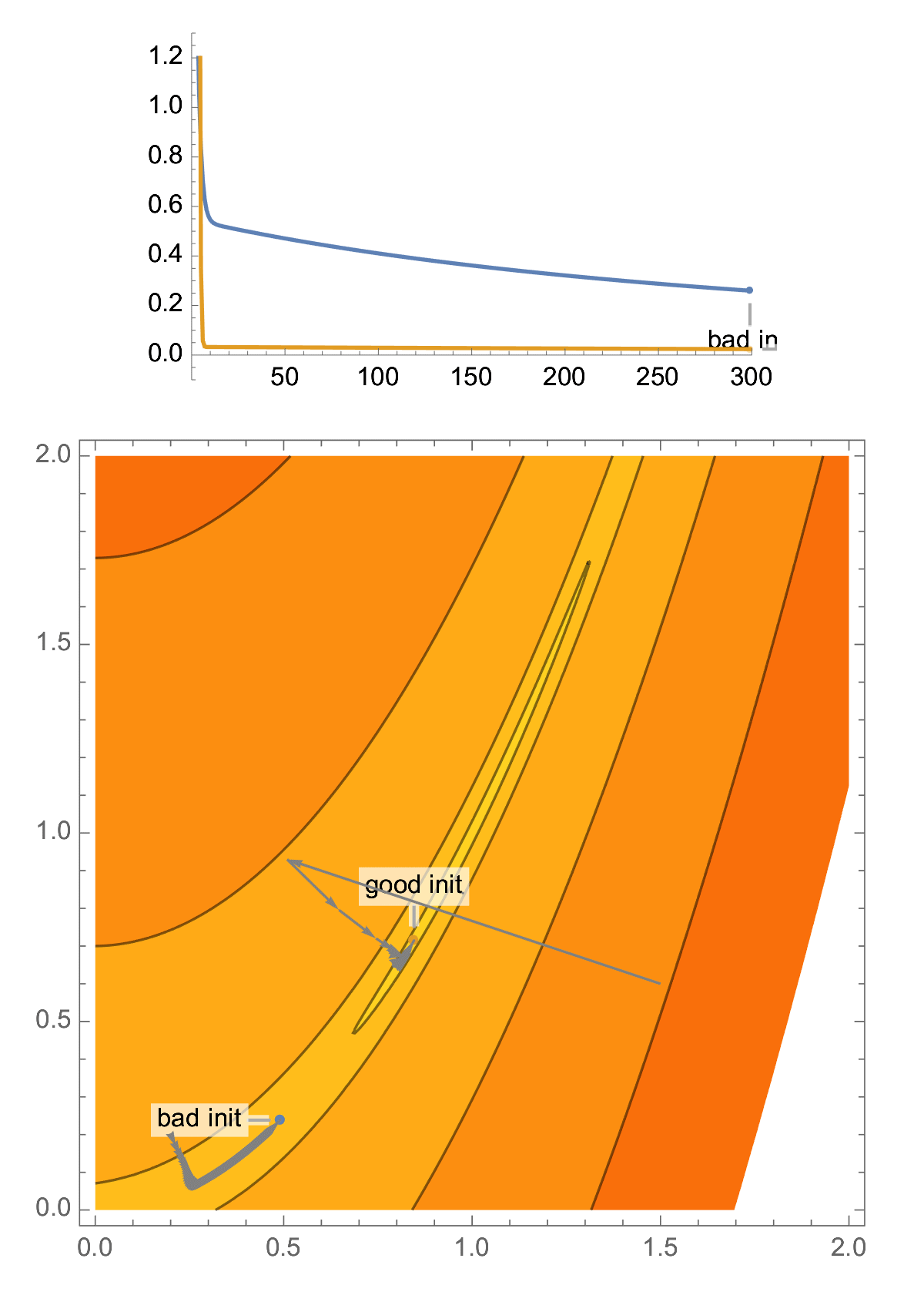
With a random initialization, it is easy to end up in the narrow valley of a 2D ill-conditioned problem, and this is the case that classical analysis of gradient descent focuses on, aka "asymptotic worst-case analysis", producing convergence rate in terms of condition number.
However, this kind of analysis is misleading in the case of high dimensions because:
- steps needed to reach asymptotic regime becomes unrealistic
- worst-case scenario becomes improbable
Take a typical ill-conditioned problem in high dimensions, with i'th eigenvalue proportional to $1/i$. This was the shape of optimization surface observed when optimizing convolutional neural networks, see Section 3.5 of "Noisy Quadratic Model" paper. For our quadratic, this is equivalent to minimizing the following function
$$x_1^2+\frac{1}{2}x_2^2+\frac{1}{3}x_3^2+\ldots$$The condition number of this problem is $n$ so as the dimensionality $n$ goes to infinity, so does the condition number. Under worst-case analysis, we would expect gradient descent to slow down to a crawl.
In practice, the opposite is true, typical gradient descent run will converge faster with more dimensions, despite condition number being worse.
To see why, take 200 random loss curves starting from random positions in a 40-dimensional problem with 1/i eigenvalue decay, with mean loss subtracted at each step.
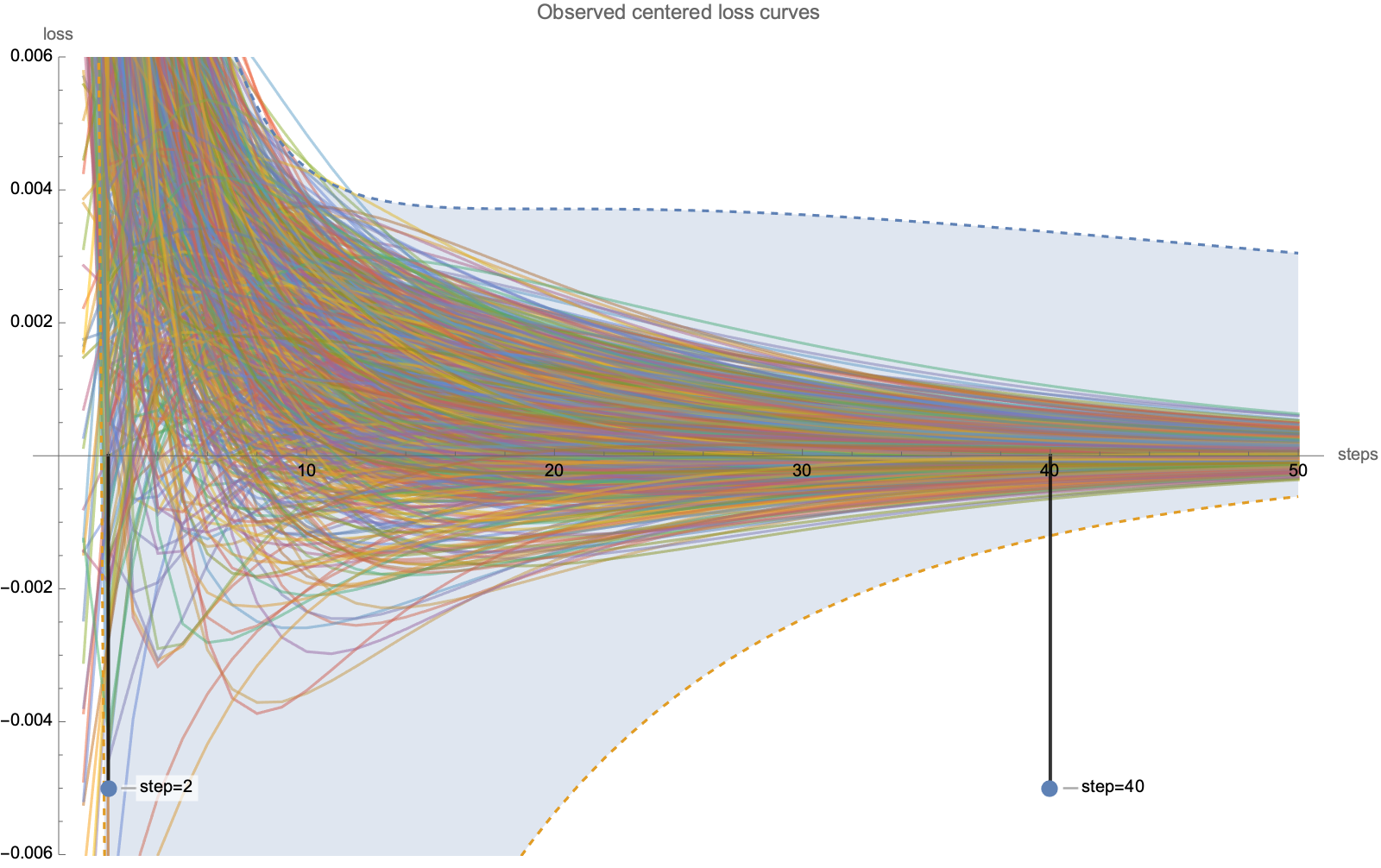
Dashed lines show best-case and worst-case scenarios, and you can see that the distribution gets concentrated around mean, far away from worst-case.
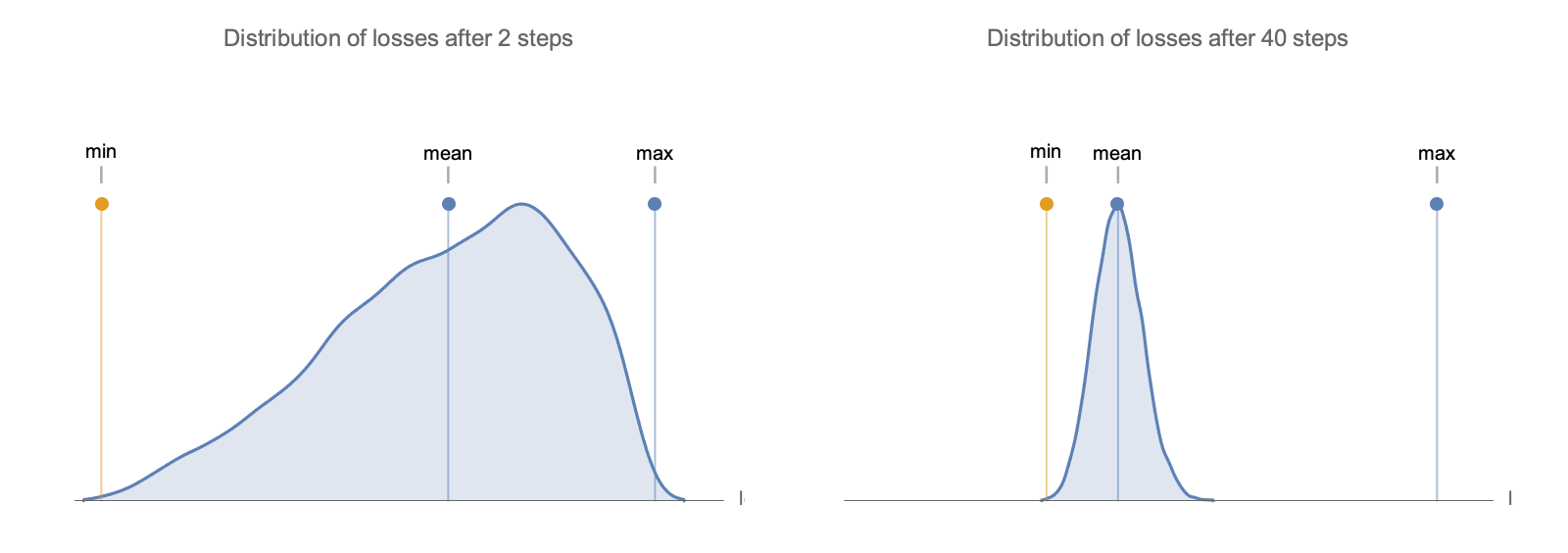
We can analyze the mean and variance of this distribution and show that loss after $s$ steps in $n$ dimensions is a linear combination of $n$ components of a Dirichlet random variable, so by weak law of large numbers, its variance goes down as $n^{-1}$ in worst case (from this and this), and as $n ^{-2}$ in the case of $1/i$ eigenvalue decay see Value of Quadratic Form on unit circle note.
Meanwhile, when dimensionality exceeds number of 2*steps, worst case behavior no longer depends on dimension, so asymptotic worst-case analysis no longer applies. See "Worst-case analysis" note.
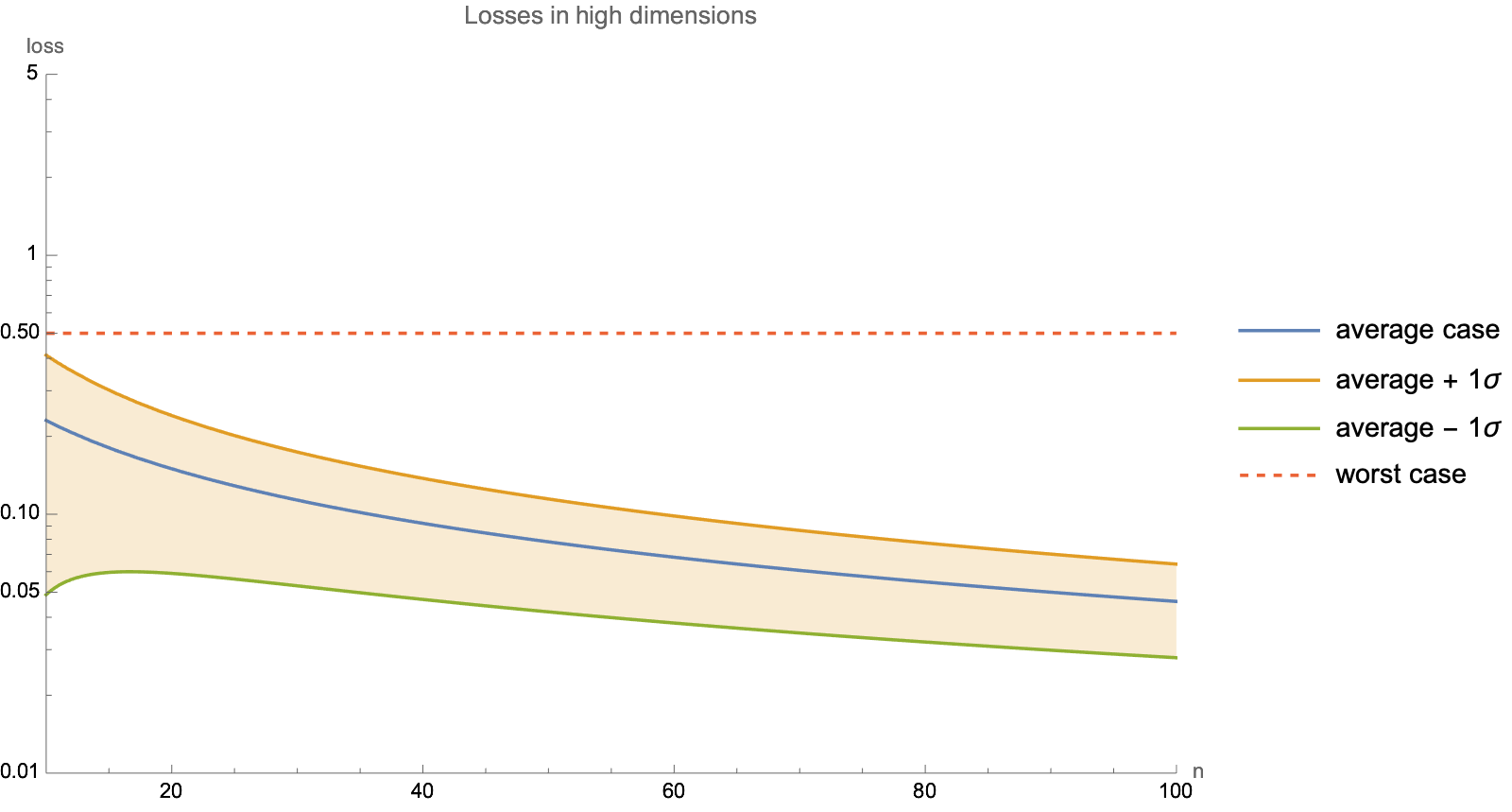
For this particular loss shape, the number of steps needed to approach exponential decay rate from standard analysis has to exceed dimensions squared $O(n^2)$. When dimensionality is huge, it's more reasonably to treat it as $O(n)$, in which case typical gradient descent path at a super-exponential rate. See "Average-case analysis" note.
(notebook)