Optimal learning rate for high-dimensional quadratic
Suppose our problem is to minimize a quadratic $y=\frac{1}{2} c x^2$ using gradient descent.
$w_{k+1}=w_k-\alpha g(w)$
Gradient descent has a learning rate parameter $\alpha$, also known as step size, what value should we use? For the problem above, you can find that using $\alpha=1/c$ takes you directly to the minimum regardless of starting position, hence it is the optimal step size in this setting. Meanwhile the largest convergent step size, ie, the value for which gradient fails to converge, is 2/c.
What about higher dimensions?
In two dimensions, you can see that the location of the starting point matters, but distance to the minimum doesn't. Hence, we can restrict ourselves to starting on the unit circle.
Consider a two dimensional quadratic:
$$\frac{1}{2}(\lambda_1 x^2 + \lambda_2 y^2)$$Since we can converge in a single step, look at the section defined by the starting point and 0. This gives us a 1-dimensional quadratic, whose curvature is between $\lambda_1$ and $\lambda_2$ depending on the starting point. Hence the “optimal” step size is between $1/\lambda_1$ and $1/\lambda_2$, and to get the average value we take expectation over possible starting points.

For instance take $\lambda_1=1$ and $\lambda_2=0.5$. Optimal step size is between 1 and 2, and $\approx 1.261$ on average. You can get a formula in terms of $\lambda_1,\lambda_2$, but it's not pretty (see notebook in the bottom).
In higher dimensions we have the following objective:
$$\frac{1}{2}(\lambda_1 x^2 +\lambda_2 y^2 + \lambda_3 z^2+\ldots)$$What should we use for coefficient values $\lambda_i$?
Roger Grosse looked at quadratic approximations of deep learning objectives, and found $\lambda_i$ to be proportional to 1/i for some practical problems, see Section 3.5 of their Noisy Quadratic Model paper. Additionally, eigenvalues of some random Hermitian matrices exhibit similar decay. Since the scale of the problem doesn't matter, normalize the problem so that largest coefficient is =1, which makes the largest convergent step size=2.
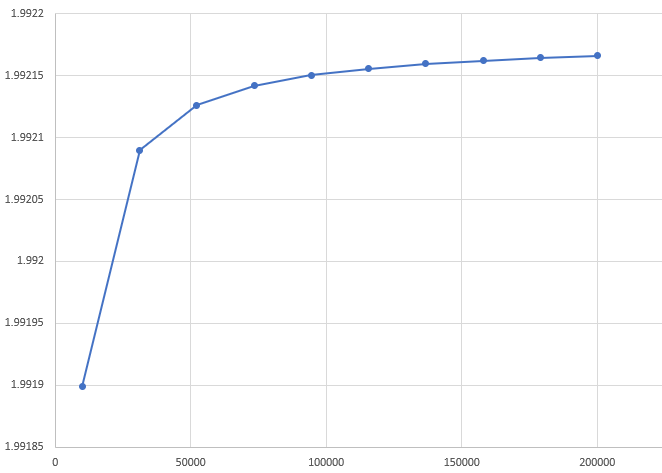
We can use numerical integration to plot the optimal step size as a function of dimensionality. Since our largest coefficient is 1, the largest convergent step size is 2. Meanwhile average optimal step size approaches 2 in high dimensions.
Mathematica notebook