How many matmuls are needed to compute Hessian-vector product of a linear neural network?
Suppose you have a simple composition of d dense functions. Computing Jacobian needs d matrix multiplications. What about computing Hessian vector product? The answer is 5*d.
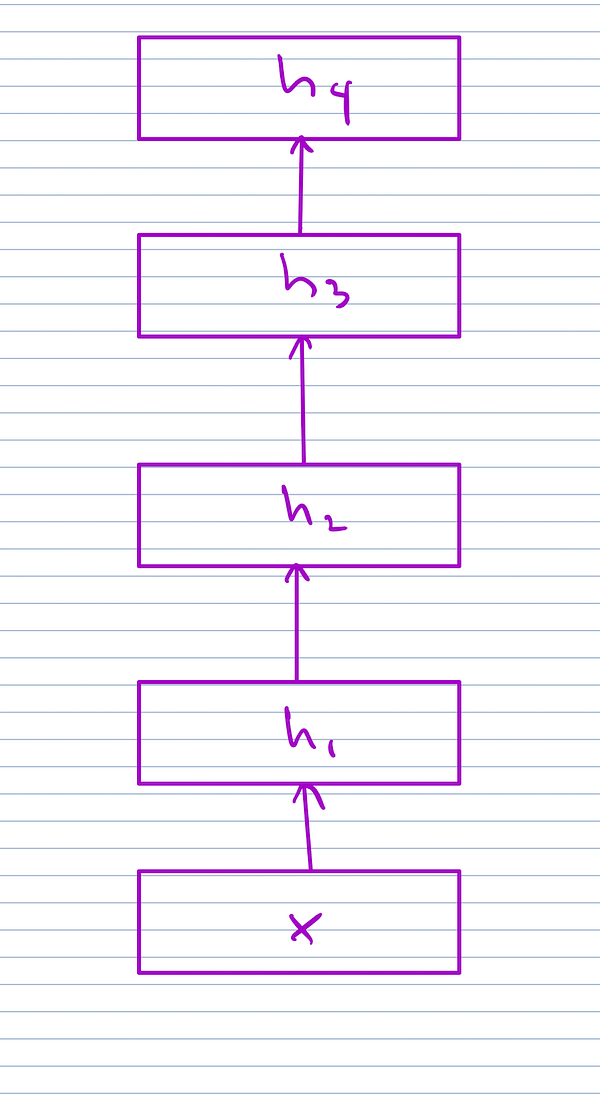
You can calculate it manually by differentiating function composition twice, grouping shared work together in temporary messages, and then counting the number of matrix multiplications. One trick to use is to note that scalar derivative equations and full multivariate versions are equivalent provided you don’t treat multiplication as commutative. So then you can simply perform derivative computations in scalar case, then the number of scalar multiplications you obtain corresponds to the number of matrix multiplications in the multivariate case.
Here’s the calculation worked out on a simple example above:

You can see there are up D temporary messages, and computing computing all the messages requires 5 multiplications, marked in purple in computation above.
Compare this against in PyTorch — create linear neural network with many layers, forward pass would require d matrix multiplications, whereas HVP would need 5*d. In practice, it takes 5-5.3x longer than forward pass, which is close to what’s expected.